Was ist die Big-O-Notation?

Die Big-O-Notation ist nicht nur ein akademisches Fachjargon – sie ist dein geheimes Werkzeug, um zu verstehen, wie sich dein Code verhält, wenn die Eingabegrößen wachsen. Stell dir vor, du baust die nächste große Social-Media-App. Dein Algorithmus funktioniert gut mit 100 Nutzern, aber was passiert, wenn es 1 Million werden? Genau hier kommt Big O ins Spiel.

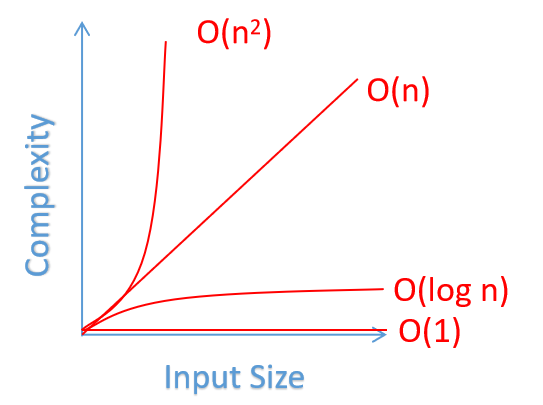
Im Kern beschreibt Big O die obere Grenze der Wachstumsrate eines Algorithmus. Es beantwortet die Frage: "Wie skaliert die Laufzeit oder der Speicherverbrauch, wenn die Eingabegröße zunimmt?" Lassen Sie uns die häufigsten Komplexitätsklassen aufschlüsseln:

• O(1): Konstante Zeit. Der Algorithmus benötigt unabhängig von der Eingabegröße die gleiche Zeit. Es ist der heilige Gral der Effizienz.
• O(log n): Logarithmische Zeit. Effizient für große Datensätze, oft in binären Suchalgorithmen zu finden.
• O(n): Lineare Zeit. Die Laufzeit wächst direkt mit der Eingabegröße. Häufig bei einfachen Iterationen.
• O(n log n): Linearithmische Zeit. Typisch für effiziente Sortieralgorithmen wie Mergesort.
• O(n^2): Quadratische Zeit. Oft in verschachtelten Schleifen zu finden. Kann bei großen Eingaben problematisch werden.
• O(2^n): Exponentielle Zeit. Der Algorithmus verdoppelt seine Laufzeit mit jeder zusätzlichen Eingabe. Wenn möglich vermeiden!

Von der Theorie zur Praxis: Analyse von echtem Code

Setzen wir unsere Detektivhüte auf und analysieren etwas Code. Betrachten Sie diese beiden Funktionen, die den Maximalwert in einem Array finden:

def find_max_naive(arr):
    max_val = arr[0]
    for i in range(len(arr)):
        for j in range(len(arr)):
            if arr[j] > max_val:
                max_val = arr[j]
    return max_val

def find_max_optimized(arr):
    return max(arr)

Auf den ersten Blick erledigen beide Funktionen die Aufgabe. Aber lassen Sie uns sie aufschlüsseln:

• find_max_naive hat verschachtelte Schleifen, was ihm eine O(n^2)-Komplexität verleiht. Autsch!
• find_max_optimized verwendet die eingebaute max()-Funktion von Python, die in O(n)-Zeit läuft.

Der Unterschied? Bei einem Array mit 1.000.000 Elementen könnte der naive Ansatz Stunden dauern, während die optimierte Version in Millisekunden fertig ist. Das ist die Macht des Verständnisses von Big O!

Zeit vs. Raum: Der ewige Kompromiss

Bei der Optimierung von Algorithmen stehen wir oft vor einem klassischen Dilemma: Priorisieren wir Geschwindigkeit (Zeitkomplexität) oder Speicherverbrauch (Raumkomplexität)? Betrachten Sie dieses Beispiel zur Berechnung von Fibonacci-Zahlen:

def fib_recursive(n):
    if n <= 1:
        return n
    return fib_recursive(n-1) + fib_recursive(n-2)

def fib_dynamic(n):
    fib = [0, 1]
    for i in range(2, n+1):
        fib.append(fib[i-1] + fib[i-2])
    return fib[n]

Die rekursive Version (fib_recursive) hat eine Zeitkomplexität von O(2^n), verwendet jedoch minimalen zusätzlichen Speicher. Der dynamische Programmierungsansatz (fib_dynamic) tauscht Speicher gegen Zeit und erreicht eine O(n)-Zeitkomplexität auf Kosten von O(n) Speicher.

Denken Sie daran: Es gibt keine universelle Lösung. Der beste Ansatz hängt von Ihren spezifischen Einschränkungen und Anforderungen ab.

Den O(n^2)-Drachen besiegen: Optimierungsstrategien

Treffen Sie auf einen O(n^2)-Algorithmus in Ihrem Code? Keine Panik! Hier sind einige Strategien, um dieses quadratische Biest zu zähmen:

1. Verwenden Sie geeignete Datenstrukturen: HashMaps können verschachtelte Schleifen in einfache Durchläufe verwandeln.
2. Teilen und Herrschen: Techniken wie die binäre Suche können die Komplexität drastisch reduzieren.
3. Caching und Memoisierung: Speichern Sie Ergebnisse, um redundante Berechnungen zu vermeiden.
4. Zwei-Zeiger-Technik: Nützlich für Array-Probleme, oft Reduzierung von O(n^2) auf O(n).

Sehen wir uns ein Beispiel zur Optimierung einer Funktion an, die Paare in einem Array mit einer gegebenen Summe findet:

# O(n^2) Lösung
def find_pairs_naive(arr, target_sum):
    pairs = []
    for i in range(len(arr)):
        for j in range(i+1, len(arr)):
            if arr[i] + arr[j] == target_sum:
                pairs.append((arr[i], arr[j]))
    return pairs

# O(n) Lösung
def find_pairs_optimized(arr, target_sum):
    seen = set()
    pairs = []
    for num in arr:
        complement = target_sum - num
        if complement in seen:
            pairs.append((num, complement))
        seen.add(num)
    return pairs

Die optimierte Version verwendet ein HashSet, um eine lineare Zeitkomplexität zu erreichen. Bei großen Arrays kann dies den Unterschied zwischen Sekunden und Millisekunden ausmachen.

Werkzeuge des Handwerks: Profiling und Analyse

Theorie ist großartig, aber manchmal braucht man kalte, harte Daten. Hier sind einige Werkzeuge, die Ihnen helfen, die Leistung Ihres Codes zu analysieren:

• Python's timeit-Modul: Ideal für schnelle Benchmarks.
• cProfile: Bietet eine detaillierte Leistungsanalyse für Python-Code.
• memory_profiler: Hilft, den Speicherverbrauch in Python-Skripten zu verfolgen.
• Big O Cheat Sheet: Ein praktisches Nachschlagewerk für gängige Algorithmen und Datenstrukturen.

Profi-Tipp: Viele IDEs, wie PyCharm, verfügen über integrierte Profiling-Tools. Nutzen Sie sie!

Best Practices für die Algorithmusoptimierung

1. Messen, nicht raten: Profilieren Sie Ihren Code immer, bevor Sie optimieren.
2. Kennen Sie Ihre Daten: Das Verständnis Ihrer Eingaben kann zu maßgeschneiderten Optimierungen führen.
3. Verwenden Sie eingebaute Funktionen: Sie sind oft hoch optimiert.
4. Seien Sie faul: Verzögern Sie Berechnungen, bis sie absolut notwendig sind.
5. Halten Sie es einfach: Manchmal ist ein einfacher Algorithmus besser als ein komplexer "optimierter".

Zusammenfassung: Das große Ganze von Big O

Das Verständnis von Big O geht nicht nur darum, schnelleren Code zu schreiben – es geht darum, intelligenteren Code zu schreiben. Es hilft Ihnen, fundierte Entscheidungen zu treffen, Skalierbarkeitsprobleme vorherzusagen und effektiv über Leistung zu kommunizieren.

Denken Sie daran, dass vorzeitige Optimierung die Wurzel allen Übels ist (oder so sagt man). Beginnen Sie immer damit, sauberen, korrekten Code zu schreiben. Wenn die Leistung dann ein Problem ist, nutzen Sie Ihre neu gewonnenen Big-O-Superkräfte, um dort zu optimieren, wo es am meisten zählt.

Gehen Sie nun hinaus und erobern Sie diese Algorithmen! Ihr zukünftiges Ich (und Ihre Nutzer) werden es Ihnen danken.

"Die erste Regel der Optimierung lautet: Tu es nicht. Die zweite Regel der Optimierung (nur für Experten) lautet: Tu es noch nicht." - Michael A. Jackson

Viel Spaß beim Programmieren, und mögen Ihre Algorithmen immer in O(1)-Zeit laufen! 🚀